※해당 시험의 출처는 인사혁신처 사이버국가 고시 센터(https://www.gosi.kr/)에 있습니다.
사용 시 출처를 꼭 표기해주시기 바랍니다.
1다음은 어느 회사의 방문 고객 수에 대한 자료이다. 산술평균, 중앙값, 최빈값을 모두 더한 값은?
2다음 사례에 해당하는 표본추출 방법은?

3확률질량함수 또는 확률밀도함수가 될 수 없는 것은?
4다음은 표본으로 조사된 5명의 양팔 길이(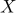 )와 키(
)와 키(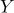 )에 대한 자료 (
)에 대한 자료 (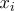 ,
, 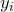 ),
), 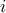 = 1,
= 1, 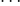 ,5 이다.
,5 이다. 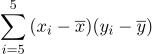 = 23.6일 때, 양팔 길이와 키의 표본상관계수는? (단, 단위는 cm이다)
= 23.6일 때, 양팔 길이와 키의 표본상관계수는? (단, 단위는 cm이다)

5어떤 확률변수 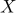 의 확률분포표가 다음과 같다. 이 모집단에서 복원추출한 크기가 2인 표본으로부터 얻은 표본평균을
의 확률분포표가 다음과 같다. 이 모집단에서 복원추출한 크기가 2인 표본으로부터 얻은 표본평균을 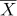 라고 하자. 표본평균
라고 하자. 표본평균 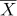 의 기댓값이
의 기댓값이 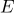 (
(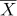 ) =
) =  일 때, 표본평균
일 때, 표본평균 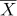 의 분산 Var(
의 분산 Var(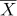 )은? (단,
)은? (단, 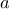 는 상수)
는 상수)

6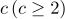 개의 범주로 나누어지는
개의 범주로 나누어지는 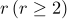 개의 다항모집단에서
개의 다항모집단에서 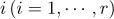 번째 모집단의 각 범주에 대한 모비율은
번째 모집단의 각 범주에 대한 모비율은 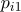 ,
, 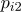 ,
, 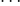 ,
, 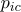 이고, 관측값은
이고, 관측값은 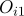 ,
, 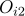 ,
, 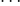 ,
, 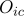 이고,
이고, 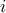 번째 모집단의 표본의 크기는
번째 모집단의 표본의 크기는 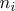 이고
이고 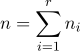 이며,
이며, 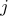 = 1,
= 1, 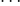 ,
,  에 대해
에 대해 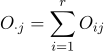 이다.
이다. 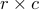 분할표의 동질성검정에 대한 설명으로 옳지 않은 것은?
분할표의 동질성검정에 대한 설명으로 옳지 않은 것은?
7질병에 대한 치료효과를 검정하기 위해 환자 10명의 치료 전과 치료 후의 검사치가 다음 표와 같다. 여기에서 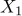 ,
, 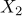 ,
, 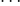 ,
,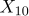 은 서로 독립이며 정규분포
은 서로 독립이며 정규분포 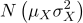 를,
를, 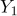 ,
, 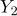 ,
, 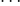 ,
, 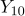 은 서로 독립이며 정규분포
은 서로 독립이며 정규분포 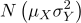 를 따른다. 치료 전후 검사치의 차의 모평균
를 따른다. 치료 전후 검사치의 차의 모평균 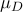 에 대해 귀무가설
에 대해 귀무가설 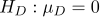 대 대립가설
대 대립가설 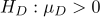 을 유의수준
을 유의수준 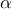 에서 검정하고자 한다. 이에 대한 설명으로 옳은 것은? (단,
에서 검정하고자 한다. 이에 대한 설명으로 옳은 것은? (단, 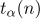 는 자유도
는 자유도 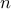 인
인 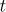 분포의 제
분포의 제 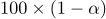 백분위수이다)
백분위수이다)

8다음은 어떤 자료를 다중선형회귀모형 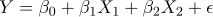 에 적합하여 얻은 결과의 일부이다. 이에 대한 설명으로 옳지 않은 것은? (단, 오차항
에 적합하여 얻은 결과의 일부이다. 이에 대한 설명으로 옳지 않은 것은? (단, 오차항  은 평균이 0이고 분산이
은 평균이 0이고 분산이 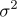 인 정규분포를 따른다)
인 정규분포를 따른다)

9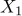 ,
, 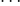 ,
, 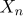 은 확률밀도함수
은 확률밀도함수 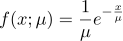 ,
, 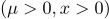 을 따르는 확률표본이다. 모수
을 따르는 확률표본이다. 모수 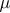 의 최대가능도추정량(maximum likelihood estimator)
의 최대가능도추정량(maximum likelihood estimator) 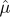 에 대한 설명으로 옳지 않은 것은? (단, log는 자연로그이다)
에 대한 설명으로 옳지 않은 것은? (단, log는 자연로그이다)
10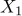 ,
, 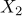 ,
, 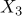 ,
, 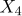 ,
, 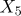 는 서로 독립이며, 구간에서 균일분포(uniform distribution)를 따르고,
는 서로 독립이며, 구간에서 균일분포(uniform distribution)를 따르고, 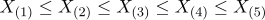 는
는 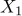 ,
, 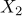 ,
, 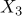 ,
, 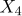 ,
, 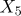 의 순서통계량이라고 할 때, 기댓값
의 순서통계량이라고 할 때, 기댓값 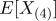 는?
는?
11전체 인구의 5%가 어떤 질병을 가지고 있다고 한다. 이 질병을 진단하는 검사 방법이 있는데, 이 검사 방법은 이 질병을 실제로 가지고 있을 때 검사 결과가 양성(positive) 반응을 나타낼 확률이 0.95, 음성(negative) 반응을 나타낼 확률이 0.05이고, 이 질병을 실제로 가지고 있지 않을 경우 검사 결과가 양성 반응을 나타낼 확률이 0.1, 음성 반응을 나타낼 확률이 0.9이다. 임의로 한 사람을 선택하여 이 검사를 한 결과가 양성 반응으로 나타났다면, 이 사람이 실제로 이 질병을 가지고 있을 확률은?
12여론조사 회사에서 어떤 사항에 대한 국민의 찬성 비율 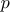 를 알아보기 위해 전화 설문조사를 무작위로 실시하려고 한다. 96% 신뢰수준에서 모든
를 알아보기 위해 전화 설문조사를 무작위로 실시하려고 한다. 96% 신뢰수준에서 모든 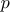 에 대한 추정량의 오차한계를 0.05이내로 하는 최소 표본의 크기
에 대한 추정량의 오차한계를 0.05이내로 하는 최소 표본의 크기 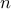 을 구하는 부등식은? (단,
을 구하는 부등식은? (단, 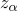 는 표준 정규분포의 제
는 표준 정규분포의 제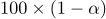 백분위수를 나타내고,
백분위수를 나타내고, 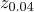 = 1.75,
= 1.75, 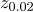 = 2.05이고, 모집단의 크기는 충분히 크다)
= 2.05이고, 모집단의 크기는 충분히 크다)
13어느 가게에 월요일부터 금요일까지 방문하는 손님 수는 다음 표와 같다. 손님 수가 요일에 따라 다른지를 검정하기 위한 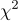 검정통계량의 값과 유의수준 5%에서 검정결과를 바르게 연결한 것은? (단,
검정통계량의 값과 유의수준 5%에서 검정결과를 바르게 연결한 것은? (단, 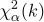 는 자유도가
는 자유도가 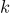 인
인 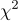 분포의 제
분포의 제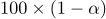 백분위수를 나타내고,
백분위수를 나타내고,  이다)
이다)

14다음은 처리 수준의 수가 5인 공정에서 처리에 따른 반응값의 모평균이 차이가 있는지를 검정하기 위한 일원배치 분산분석법을 적용한 결과의 일부이다. 검정에 대한 유의확률(significance probability) 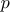 의 범위는? (단,
의 범위는? (단, 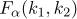 는 분자의 자유도가
는 분자의 자유도가 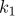 이고 분모의 자유도가
이고 분모의 자유도가 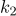 인
인 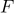 분포의 제
분포의 제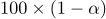 백분위수를 나타내고,
백분위수를 나타내고,  이다)
이다)

15관측된 자료 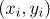 ,
, 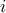 = 1,
= 1, 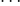 , 21에서 얻은 통계량의 값이
, 21에서 얻은 통계량의 값이 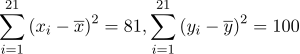 이다. 이 자료를 단순선형 회귀모형
이다. 이 자료를 단순선형 회귀모형 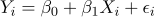 에 적합하여 얻은 기울기에 대한 최소제곱추정값이
에 적합하여 얻은 기울기에 대한 최소제곱추정값이 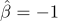 일 때, 이에 대한 설명으로 옳은 것은? (단, 오차항
일 때, 이에 대한 설명으로 옳은 것은? (단, 오차항 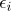 는 서로 독립이며 정규분포
는 서로 독립이며 정규분포 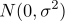 을 따른다)
을 따른다)
16처리 수준의 수가 4인 인자 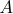 와 처리 수준의 수가 2인 인자
와 처리 수준의 수가 2인 인자 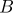 에 대한 반복이 없는 이원배치법의 실험에서 다음과 같은 자료를 얻었다. 분산분석 결과에서 인자
에 대한 반복이 없는 이원배치법의 실험에서 다음과 같은 자료를 얻었다. 분산분석 결과에서 인자 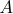 와 인자
와 인자 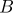 가 모두 유의수준
가 모두 유의수준
5%에서 유의한 것으로 판명되었다. 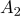 수준과
수준과 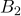 수준을 조합한 실험 조건에서 모평균의 추정값은?
수준을 조합한 실험 조건에서 모평균의 추정값은?
5%에서 유의한 것으로 판명되었다.

17숫자 1, 2, 3, 4가 표시된 공정한 정사면체 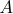 ,
, 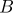 두 개를 던져서 나오는 눈의 수를 각각
두 개를 던져서 나오는 눈의 수를 각각 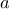 ,
, 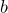 라고 하고, 확률변수
라고 하고, 확률변수 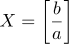 라고 할 때, 확률변수
라고 할 때, 확률변수 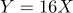 의 기댓값은? (단, [
의 기댓값은? (단, [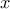 ]는
]는 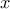 보다 크지 않는 최대 정수를 나타낸다)
보다 크지 않는 최대 정수를 나타낸다)
18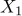 ,
, 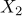 ,
, 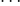 ,
, 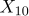 은 평균이 0, 분산이 4인 정규모집단으로부터 추출한 확률표본이고,
은 평균이 0, 분산이 4인 정규모집단으로부터 추출한 확률표본이고, 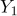 ,
, 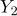 ,
, 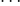 ,
, 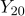 은 평균이 0, 분산이 8인 정규모집단으로부터 추출한 확률표본이다. 두 모집단이 독립일 때, 표본평균
은 평균이 0, 분산이 8인 정규모집단으로부터 추출한 확률표본이다. 두 모집단이 독립일 때, 표본평균 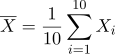 와
와 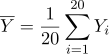 를 이용한 통계량
를 이용한 통계량 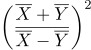 의 확률분포는?
의 확률분포는?
19어느 자료에서 변수 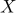 와
와 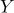 를 평균이 0, 표준편차가 1이 되도록 각각 표준화한 변수를
를 평균이 0, 표준편차가 1이 되도록 각각 표준화한 변수를 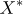 와
와 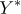 라 하자. 설명변수
라 하자. 설명변수 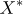 와 반응변수
와 반응변수 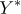 를 절편이 있는 단순선형회귀모형에 적용하여 얻은 추정회귀식과 분산분석표에 대한 설명으로 옳은 것만을 모두 고르면?
를 절편이 있는 단순선형회귀모형에 적용하여 얻은 추정회귀식과 분산분석표에 대한 설명으로 옳은 것만을 모두 고르면?

20







