1다음 <보기> 중 항상 닮은 도형인 것은 모두 몇 개인가?
<보기>
ㄱ. 두 원 ㄴ. 두 정사각형
ㄷ. 두 마름모 ㄹ. 두 직각삼각형
ㅁ. 두 정삼각형 ㅂ. 두 사면체
ㅅ. 두 정육면체 ㅇ. 두 원뿔
ㅈ. 두 구 ㅊ. 두 원기둥
2원 O 와 원 O' 의 닮음비가 3 : 2 이고 원 O' 의 반지 름의 길이가 6cm 일 때, 원 O 의 둘레의 길이는?
3다음 그림과 같이 지름이 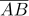 인 반원 O 에서 두 점 C , D 는 각각
인 반원 O 에서 두 점 C , D 는 각각 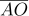 ,
, 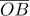 의 중점이다. 지름이
의 중점이다. 지름이 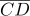 인 반원의 넓이가 20 ㎠일 때, 색칠한 부분의 넓이를 구하여라.
인 반원의 넓이가 20 ㎠일 때, 색칠한 부분의 넓이를 구하여라.

4다음 표는 어느 가게에서 파는 수박 A , B 의 지름의 길 이와 가격을 나타낸 것이다. 이 가게에서 2 만 원으로 수 박 A 를 2 통 사는 것과 수박 B 를 1 통 사는 것 중 어 느 것이 더 유리한가? (단, 수박은 구로 생각하고 껍질의 두께는 무시한다.)

5다음 그림과 같은 두 직육면체가 서로 닮음일 때, x , y 의 값을 구하여라.

6다음 중 항상 닮은 도형이라고 할 수 없는 것은?
7다음 그림과 같은 원뿔의 모선 OA 의 삼등분점 C 를 지 나고 윗면에 평행인 평면으로 잘라 낸 원뿔대 모양의 그릇 에 모선 OA의 삼등분점 B 까지 물이 채워져 있다. 모 선이 OA 인 원뿔의 부피가 54π ㎤일 때, 물의 부피 는?

8다음 그림과 같이 원뿔을 밑면에 평행한 평면으로 잘라서 생기는 작은 원뿔의 밑면의 반지름의 길이는?

9다음 그림과 같이 서로 닮음인 두 원 O , O' 의 반지름의 길이의 비가 4 : 5 이고 원 O 의 넓이가 64 π ㎠일 때, 원 O' 의 넓이는?

10다음 그림에서 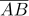 =
= 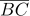 =
= 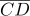 이고,
이고, 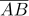 ,
, 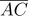 , 는 각각 세 원의 지름이다. 가장 작은 원의 넓이가 4㎠ 일 때, 색칠한 부분의 넓이를 구하여라.
, 는 각각 세 원의 지름이다. 가장 작은 원의 넓이가 4㎠ 일 때, 색칠한 부분의 넓이를 구하여라.






