1다음 그림에서 점 O 는 △ABC의 외심이다. ∠BOC = 140°일 때, ∠BAC 의 크기는?
2다음 그림에서 △ABC는 ∠A=90° 인 직각삼각형이고 원 O 는 △ABC 의 외접원, 원 I 는 △ABC 의 내접원이다.
두 원 O , I 의 반지름의 길이가 각각 3 cm , 1 cm 일 때, △ABC의 넓이는?
3다음 그림과 같이 ∠C=90° 인 직각삼각형 ABC 에서 점 M 은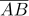 
의 중점이고 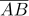=28cm , ∠B= 50°일 때, 다음 중 옳지 않은 것은?
4다음 그림에서 점 I 는 △ABC 의 내심이다. ∠IBC= 20° , ∠ICB=32°일 때, ∠IAD의 크기는?
5다음 그림에서 점 I 가 △ABC의 내심이다.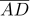 
=2 cm , 
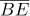= 4 cm , 
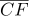= 3 cm 일 때, △ABC 의 둘레의 길이를 구하여라.
6아래 그림과 같이 △ABC 의 세 내각의 이등분선이 한 점 I 에서 만날 때, 다음 중 옳지 않은 것은?
7다음 그림에서 점 O 는 △ABC의 외심이다. ∠ACB=30° , ∠OCB=10°일 때, ∠x 의 크기를 구하여라.
8다음 그림에서 점 I 는 △ABC 의 내심이고,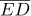 
// 
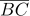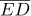이다. = 17 cm , 
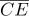= 10 cm 일 때, 
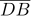의 길이 를 구하여라.
9다음 그림과 같은 △ABC 에서 점 O 는 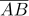와 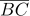의 수직이등분선의 교점이고 ∠ABO=32° , ∠OBC=30°일 때, ∠BAC 의 크기를 구하여라.
10다음 그림에서 점 O 는 △ABC 의 외심이다. ∠A=55°일 때, ∠x 의 크기를 구하여라.
연결된 장치가 없습니다.
